കൈപ്പിടിയിലൊതുക്കാം, കണക്കിനെ

80 മാർക്ക്

സമയം 2.30 മണിക്കൂർ

നിർദേശങ്ങൾ

ഉത്തരങ്ങൾ എഴുതുന്നതിന് മുമ്പ് ഓരോ ചോദ്യവും ശ്രദ്ധയോടെ വായിക്കണം. ആവശ്യമുള്ളയിടത്ത് വേണ്ട രീതിയിലുള്ള വിശദീകരണങ്ങൾ നൽകിയിരിക്കണം. ആദ്യത്തെ 15 മിനുട്ട് സമാശ്വാസ സമയമാണ്. ഈ സമയത്ത് ചോദ്യങ്ങൾ ശ്രദ്ധയോടെ വായിച്ച് ഉത്തരങ്ങൾ കണ്ടെത്തി വെക്കണം.

സെക്ഷൻ എയിലെ എല്ലാ ചോദ്യങ്ങൾക്കും ഉത്തരമെഴുതണം. ഒരു സ്കോർ വീതം

                                                                                             സെക്ഷൻ A

1. താഴെ കൊടുത്തിരിക്കുന്ന ശ്രേണിയിലെ (4, 9, 14, …) രണ്ട് പദങ്ങൾ തമ്മിലുള്ള വ്യത്യാസമായി വരാത്തത് ഏതാണ്?

(45, 50, 55, 58)

2. ആദ്യത്തെ അഞ്ച് അഭാജ്യ സംഖ്യകളുടെ (prime numbers) മാധ്യം (mean) എത്രയാണ്?

(14, 9, 15, 13)

3. താഴെ കൊടുത്തിരിക്കുന്ന ബിന്ദുക്കളിൽ (points) ഏതിനാണ് ആധാരബിന്ദുവിൽ (origin) നിന്നുള്ള ദൂരം അഞ്ച് യൂണിറ്റിൽ കുറവുള്ളത്?

[(3,4), (2,6), (4,3), (1,4)]

4. ഉയരം 9 സെ. മീ. ഉള്ള ഒരു ശരിയായ വൃത്തസ്തൂപത്തിന്റെ (right circular cone) വ്യാപ്തം 48cm3 ആണെങ്കിൽ, അതിന്റെ വ്യാസം (diameter) കണ്ടെത്തുക.

(12 സെ.മീ., 10സെ.മീ., 6 സെ.മീ., 8 സെ.മീ.)

5. ആദ്യത്തെ 19 എണ്ണൽ സംഖ്യകളുടെ (natural numbers) ആകെ തുക 190 ആണ്. എങ്കിൽ ആദ്യത്തെ 20 എണ്ണൽ സംഖ്യകളുടെ തുക എത്ര?

(200, 201, 210, 211)

6. പൊതു വ്യത്യാസം (common difference) 6 ആയുള്ള ഒരു സമാന്തരശ്രേണിയിലെ തുടർച്ചയായ രണ്ട് സംഖ്യകളുടെ ഗുണനഫലം 280 ആണ്.

a) ഒരു സംഖ്യയെ x ആയി എടുത്താൽ, മറ്റേ സംഖ്യ = ______

b) സമവാക്യം (equation) രൂപപ്പെടുത്തുക.

7. പ്രസ്താവന i): ഒരു മട്ടത്രികോണത്തിന്റെ ലംബമായ വശങ്ങൾ 3 മീറ്റർ വീതം ആണെങ്കിൽ, അതിന്റെ കർണ്ണം 3√2 ആണ്.

പ്രസ്താവന ii) 45 : 45: 90 കോണുകളുള്ള ഏതൊരു ത്രികോണത്തിലും ചെറുവശങ്ങൾ ഒരേ നീളമുള്ളവയാണ്. ഏറ്റവും നീളം കൂടിയ വശം ആ നീളത്തിന്റെ √2 ഇരട്ടിയാണ്.

8) പ്രസ്താവന i):
P (a , 4) എന്ന ബിന്ദു A(- 6, 5) ഉം B (-4, 3)
2 യുമായി
ചേരുന്ന വര മധ്യബിന്ദുവാണെങ്കിൽ Aയുടെ മൂല്യം -10 ആയിരിക്കും

പ്രസ്താവന ii): (x1, y1) , (x2, y2) ഉം ആയ രണ്ട് ബിന്ദുക്കളെ ചേർക്കുന്ന വരയുടെ മധ്യബിന്ദു
(x1+ x2 ഉം y1+y2) ഉം ആയിരിക്കും.
2 2

7, 8 എന്നീ ചോദ്യങ്ങൾക്ക് ഉചിതമായത് താഴെ പറയുന്നവയിൽ നിന്ന് തിരഞ്ഞെടുത്തെഴുതുക.

a) പ്രസ്താവന I ശരിയാണ്, II തെറ്റാണ്.

(b) പ്രസ്താവന I തെറ്റാണ്, II ശരിയാണ്.

(c) പ്രസ്താവന I ഉം II ഉം ശരിയാണ്, എന്നാൽ II പ്രസ്താവന Iന് ശരിയായ വിശദീകരണം അല്ല.

(d) പ്രസ്താവന I ഉം II ഉം ശരിയാണ്, II പ്രസ്താവന I ന് ശരിയായ വിശദീകരണമാണ്.

 സെക്ഷൻ B

9. 10 സെ.മീ വശമുള്ള ഒരു ചതുരത്തിനുള്ളിൽ ഒരു കുത്ത് ഇട്ടിരിക്കുന്നു. ഈ ചതുരത്തിനുള്ളിൽ വരയ്ക്കാൻ കഴിയുന്ന ഏറ്റവും വലിയ വൃത്തത്തിനുള്ളിൽ ആ കുത്ത് വരാനുള്ള സാധ്യത കണ്ടെത്തുക (1)

10. ഒരു സമാന്തര ശ്രേണിയുടെ 5ാം പദത്തിന്റെയും 8ാം പദത്തിന്റെയും തുക 62 ആണ്.

(a) ഈ ശ്രേണിയുടെ 1ാം പദവും 10ാം പദവും ചേർന്ന തുക കണ്ടെത്തുക. (1)

(b) ഈ ശ്രേണിയുടെ ആദ്യത്തെ 10 പദങ്ങളുടെ തുക കണ്ടെത്തുക. (1)

(c) ഈ ശ്രേണിയുടെ 9ാം പദം 52 ആണെങ്കിൽ, അതിന്റെ 2ാം പദം കണ്ടെത്തുക. (1)

11. A) രണ്ട് ഡൈസ് ഒരേസമയം എറിയുന്നു. താഴെ പറയുന്ന രീതിയിൽ വരാനുള്ള സാധ്യത കണ്ടെത്തുക.

(a) ആദ്യ ഡൈസിൽ ഒരു ഇരട്ടസംഖ്യ ലഭിക്കാനുള്ള സാധ്യത (1)

(b) ലഭിക്കുന്ന തുക ഒരു ഇരട്ടസംഖ്യ ആയിരിക്കാനുള്ള സാധ്യത (1)

(c) ലഭിക്കുന്ന തുക 6 ൽ കുറവായിരിക്കാനുള്ള സാധ്യത (1)

            അല്ലെങ്കിൽ

B) ഒരു പെട്ടിയിൽ കറുത്തതും വെളുത്തതും ആയി ആകെ 24 മുത്തുകൾ ഉണ്ട്. ഇതിൽ നിന്നും ഒരു മുത്തെടുത്താൽ അത് കറുത്തതാകാനുള്ള സാധ്യത 1/4 ആണ് എങ്കിൽ

a) കറുത്ത മുത്തുകളുടെ എണ്ണം (1)

b) വെളുത്ത മുത്തുകളുടെ എണ്ണം (1)

c) എത്ര കറുത്ത മുത്തുകൾ കൂടി ഇതിലേക്ക് ഇട്ടാൽ കറുത്ത മുത്ത് കിട്ടാനുള്ള സാധ്യത 1/3 ആകും (1)

12. ഒരു സമാന്തര ശ്രേണിയിലെ ആദ്യ 5 പദങ്ങളുടെ തുക 55 ആണ്. അതുപോലെ, ആദ്യ 10 പദങ്ങളുടെ തുക 185 ആണ്.

a) ഈ ശ്രേണിയിലെ 3ാം പദം എത്ര? (1)

b) ഈ ശ്രേണിയിലെ 8ാം പദം എത്ര? (1)

c) ഈ ശ്രേണിയിലെ ആദ്യ 15 പദങ്ങളുടെ തുക എത്ര? (2)

അല്ലെങ്കിൽ

ഒരു സമാന്തര ശ്രേണിയുടെ ബീജഗണിത രൂപം 5n + 2 ആണെങ്കിൽ,

a) ഈ ശ്രേണിയുടെ പൊതുവ്യത്യാസം (Common difference) എത്ര?

b) ഈ ശ്രേണിയിലെ 20ാം പദം എത്ര?

c) ഈ ശ്രേണിയിലെ ആദ്യ 20 പദങ്ങളുടെ തുക എത്ര?

13. താഴെ നൽകിയിരിക്കുന്ന പട്ടികയിൽ ശ്രീലക്ഷ്മി കുടുംബശ്രീ യൂണിറ്റിലെ അംഗങ്ങളെ അവരുടെ പ്രായം അനുസരിച്ച് തരംതിരിച്ച് കാണിച്ചിരിക്കുന്നു. (5)

a) അംഗങ്ങളെ പ്രായം കൂടുന്ന ക്രമത്തിൽ ക്രമീകരിച്ചാൽ, ആരുടെ പ്രായം ആകും മധ്യമം ആകുക

b) 38ാം സ്ഥാനത്തുള്ള അംഗത്തിന്റെ പ്രായം എത്രയായിരിക്കും?

c) അംഗങ്ങളുടെ പ്രായങ്ങളുടെ മധ്യമം (Median) കണ്ടെത്തുക.

         സെക്ഷൻ സി

14. A(3, 2)യും B(13, 7)യും AB എന്നീ ബിന്ദുക്കൾ യോജിപ്പിക്കുന്ന AB വരയിൽ

A) AP : PB = 3 : 2 ആകുന്ന രീതിയിലുള്ള P എന്ന ബിന്ദുവിന്റെ സൂചക സംഖ്യ കാണുക. (1)

B) AB എന്ന വരയുടെ ചരിവ് കണ്ടെത്തുക. (1)

C) AB എന്ന വരയുടെ സമവാക്യം കണ്ടെത്തുക. (2)

15. x, y അക്ഷങ്ങൾ വരച്ച് (-1, 1)യും (-5, 5)യും എന്നീ ബിന്ദുക്കൾ അടയാളപ്പെടുത്തുക. (2)

A) ഇവയെ ഒരു ചതുരത്തിന്റെ എതിർ മൂലകളായി എടുത്താൽ ചതുരത്തിന്റെ മറ്റ് രണ്ട് എതിർ മൂലകളുടെ സൂചക സംഖ്യകൾ എഴുതുക. (1)

       അല്ലെങ്കിൽ

B) ഒരു ചതുരത്തിന്റെ വശങ്ങൾ അക്ഷങ്ങൾക്ക് സമാന്തരമാണ്. അതിന്റെ ഒരു ജോഡി എതിർമൂലകൾ (4,6), (8,14) എന്നിവയാണ്.

i) ചതുരത്തിന്റെ മറ്റ് രണ്ട് മൂലകളുടെ സൂചക സംഖ്യകൾ എഴുതുക

ii) വികർണങ്ങൾ കൂട്ടിമുട്ടുന്ന ബിന്ദുവിന്റെ സൂചകസംഖ്യകൾ എഴുതുക

iii) വികർണങ്ങളുടെ നീളം കണക്കാക്കുക

16. ഒരു വൃത്തത്തിന്റെ സമവാക്യം x2+y2- 8x-6y +9=0

i) വൃത്ത കേന്ദ്രത്തിന്റെ സൂചക സംഖ്യകൾ കണ്ടെത്തുക. (2)

ii) വൃത്തത്തിന്റെ ആരം കണ്ടെത്തുക. (1)

iii) വൃത്തത്തിൽ വരുന്ന രണ്ട് ബിന്ദുക്കൾ കണ്ടെത്തുക. (1)

  അല്ലെങ്കിൽ

ഒരു വൃത്തത്തിന്റെ കേന്ദ്രം C(4, 4) ആണ്. ആ വൃത്തത്തിന്റെ X അക്ഷവും Y അക്ഷവും യഥാക്രമം A, B ബിന്ദുക്കളിൽ കൂടി തൊടുന്നു.

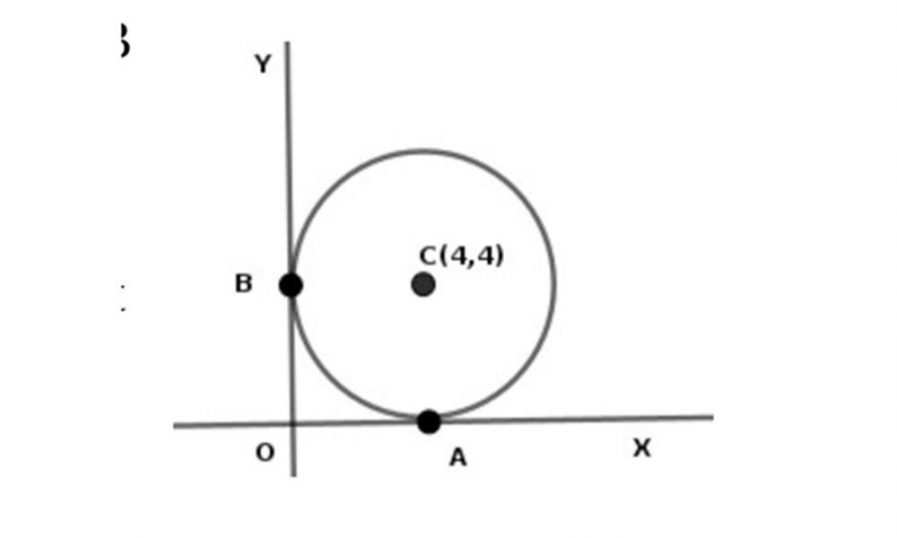
A) A, B ബിന്ദുക്കളുടെ സൂചക സംഖ്യകൾ കണ്ടെത്തുക. (2)

B) വൃത്തത്തിന്റെ ആരം കണ്ടെത്തുക. (1)

C) വൃത്തത്തിന്റെ സമവാക്യം കണ്ടെത്തുക. (1)

  സെക്ഷൻ ഡി

17. ഒരു മട്ട ത്രികോണത്തിന്റെ വശങ്ങളുടെ നീളം, ഏറ്റവും ചെറിയ വശത്തിന്റെ നീളത്തിന്റെ ഇരട്ടിയേക്കാൾ 6 സെ.മീ. കൂടുതലാണ്. മറ്റൊരു വശത്തിന്റെ നീളം, ഏറ്റവും ചെറിയ വശത്തിന്റെ നീളത്തിന്റെ മൂന്നു ഇരട്ടിയിൽ നിന്ന് 6 സെ.മീ. കുറവാണ്. എങ്കിൽ ആ ത്രികോണത്തിന്റെ വശങ്ങളുടെ നീളങ്ങൾ കണ്ടെത്തുക. (3)

18. A) 100, 109, 118, … എന്ന സമാന്തര ശ്രേണിയിലെ 10ാം പദം കണ്ടെത്തുക. (1)

B) 9 ന്റെ ഗുണിതങ്ങളായ മൂന്ന് അക്ക സംഖ്യകളുടെ ശ്രേണി എഴുതുക. (1)

C) 9 ന്റെ ഗുണിതങ്ങളായ മൂന്ന് അക്ക സംഖ്യകളുടെ സമാന്തര ശ്രേണിയിൽ 999 എന്ന സംഖ്യയുടെ സ്ഥാനം (position) കണ്ടെത്തുക. (2)

     അല്ലെങ്കിൽ

B) താഴെ കൊടുത്തിരിക്കുന്നവയുടെ തുക കണ്ടെത്തുക:

a) 1 + 2 + 3 + 4 + … + 100 = ? (1)

b) 1 + 3 + 5 + … + 99 = ? (1)
c) 2 + 4 + 6 + … + 100 = ? (1)

d) 3 + 7 + 11 + … + 99 = ? (1)

19. ഒരു സമാന്തര ശ്രേണിയുടെ തുകയുടെ ബീജഗണിത രൂപം 3n2-4n ആണ്.

a) ആദ്യ പദം കണ്ടെത്തുക. (1)

b) ശ്രേണിയുടെ ബീജഗണിത രൂപം (general term) എഴുതുക. (2)

c) ഈ ശ്രേണിയിലെ ആദ്യ 30 പദങ്ങളുടെ തുക കണ്ടെത്തുക. (1)

              അല്ലെങ്കിൽ

a) പൊതുവ്യത്യാസം 6 ആയ ഒരു സമാന്തര ശ്രേണിയുടെ ആദ്യ 20 പദങ്ങളുടെ ആകെ തുക 1300 ആണ്. സമാന്തര ശ്രേണി എഴുതുക. (2)

b) ഈ സമാന്തര ശ്രേണിയുടെ ആദ്യ 21 പദങ്ങളുടെ ആകെ തുക കണ്ടെത്തുക. (1)

ഈ സമാന്തര ശ്രേണിയുടെ ബീജഗണിത രൂപം എഴുതുക. (1)

  സെക്ഷൻ ഇ

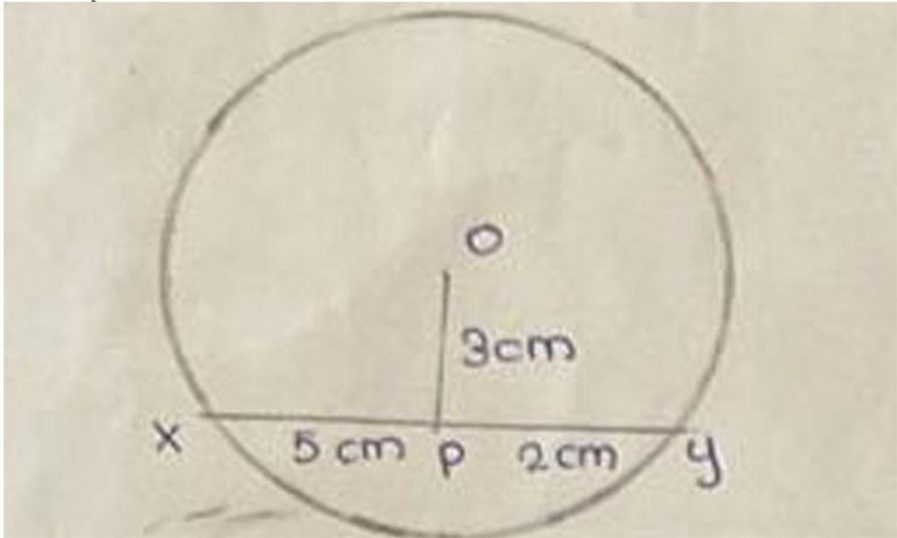
20. നൽകിയിരിക്കുന്ന ചിത്രത്തിൽ O വൃത്തത്തിന്റെ കേന്ദ്രമാണ്.
OP = 3 സെ.മീ., XP = 5 സെ.മീ., PY = 2 സെ.മീ. ആണെങ്കിൽ, വൃത്തത്തിന്റെ ആരം കണ്ടെത്തുക. (2)

21. A). p(x)= -x2- 7x+ 13. p(3)യുടെ വില കണ്ടെത്തുക (1)

B). P(x)- P(3) എന്ന ബഹുപദത്തിനെ ഒന്നാംകൃതി ഘടകങ്ങളാക്കി എഴുതുക. (2)

22. ചിത്രത്തിൽ O, O’ വൃത്ത കേന്ദ്രങ്ങളാണ്. P, R എന്നീ ബിന്ദുക്കൾ രണ്ട് വൃത്തങ്ങൾ കൂട്ടിമുട്ടുന്ന ബിന്ദുക്കളാണ്.
<PQR- 800 ആണെങ്കിൽ താഴെ പറയുന്ന കോണളവുകൾ എഴുതുക. (3)

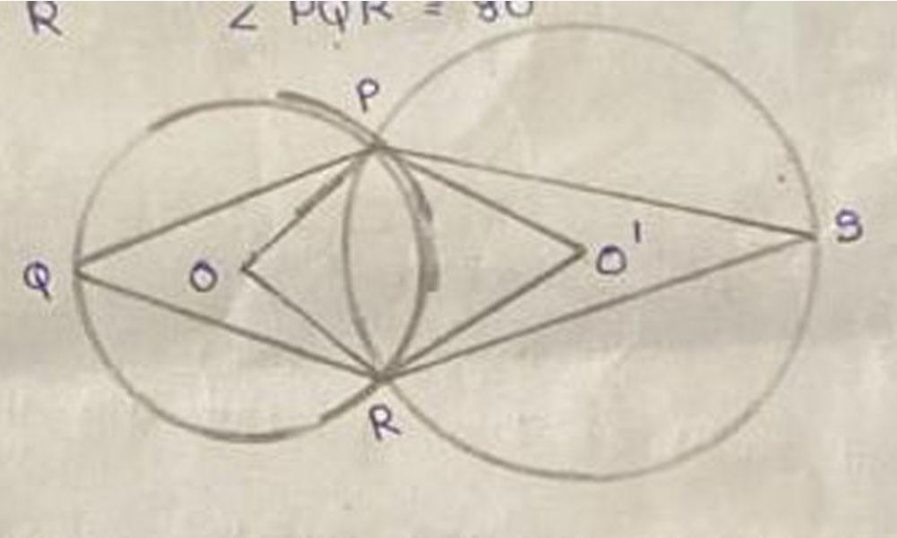
i) <POR=
ii) <PSR =
iii) <PO’R കണ്ടെത്തുക.

23. 90 മീറ്റർ ഉയരമുള്ള ഒരു ടവറിന്റെ മുകളിൽ നിന്ന് ഒരാൾ ഒരു കെട്ടിടത്തിന്റെ മുകളിലത്തെ ഭാഗം 500 മേൽ കോണിലും (angle of elevation) അതിന്റെ അടിഭാഗം 300 കീഴ് കോണിലും (angle of depression) കാണുന്നു. (4)

i) ഒരു ഏകദേശ ചിത്രം വരയ്ക്കുക.

ii) ടവറും കെട്ടിടവും തമ്മിലുള്ള അകലം കണ്ടെത്തുക.

iii) ടവറിന്റെ മുകളിൽ നിന്ന് കെട്ടിടത്തിന്റെ അടിഭാഗത്തേക്കുള്ള ദൂരം കണ്ടെത്തുക.

iv) കെട്ടിടത്തിന്റെ ഉയരം കണ്ടെത്തുക.

 അല്ലെങ്കിൽ

ഒരു കനാലിന്റെ അരികിൽ നിൽക്കുന്ന 1.5 മീറ്റർ ഉയരമുള്ള ഒരു ബാലൻ, കനാലിന്റെ മറുവശത്തുള്ള ഒരു വൃക്ഷത്തിന്റെ മുകളിലത്തെ ഭാഗം 700 മേൽ കോണിൽ കാണുന്നു. 10 മീറ്റർ പിന്നോട്ട് മാറി നിന്നപ്പോൾ, അതേ വൃക്ഷത്തിന്റെ മുകളിലത്തെ ഭാഗം 250 മേൽ കോണിൽ കാണുന്നു.

i) ഒരു ഏകദേശ ചിത്രം വരയ്ക്കുക.

ii) വൃക്ഷത്തിന്റെ ഉയരം കണ്ടെത്തുക.

iii) കനാലിന്റെ വീതി കണ്ടെത്തുക.

24. A). ഒരു വൃത്തത്തെ തൊടുന്ന രീതിയിൽ ABCD എന്ന ചതുർഭുജം വരച്ചിരിക്കുന്നു. AB, BC, CD, AD എന്ന വശങ്ങൾ യഥാക്രമം PQRS ബിന്ദുക്കളിൽ വൃത്തത്തെ തൊടുന്നു. (4)

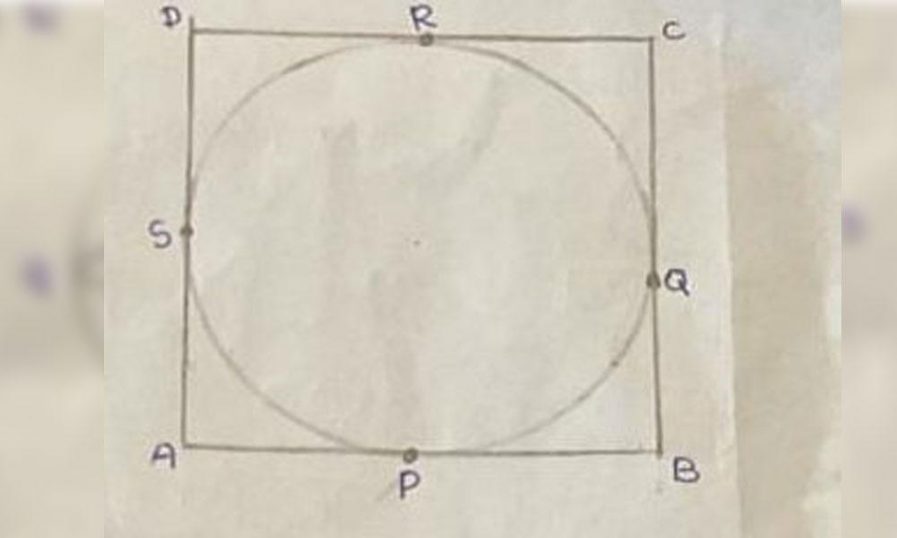
i) AB+CD= AD+BC

ii) AB = C സെ മി, BC = 7 സെ.മീ, CD = 3 സെ.മീ, AD = 5 സെ.മീ ആയാൽ X കണ്ടെത്തുക.

  അല്ലെങ്കിൽ

 

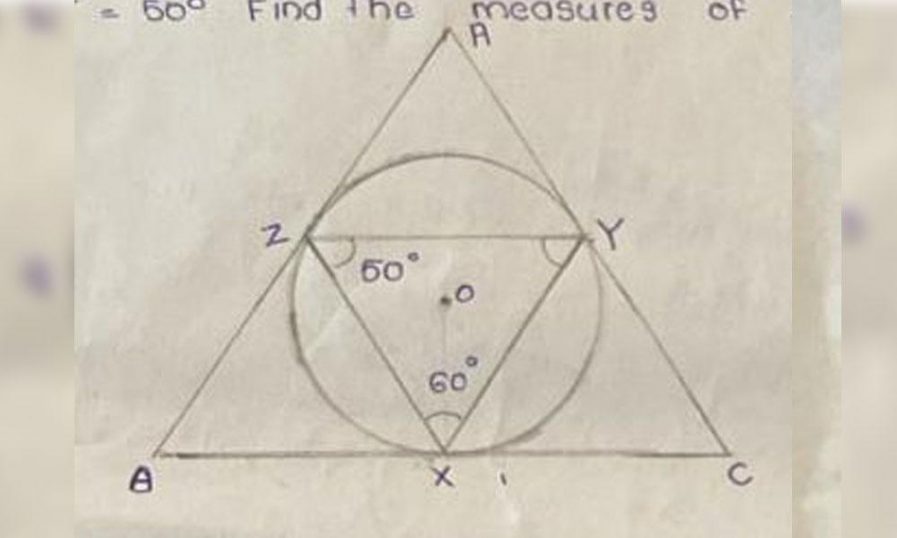
B). ഒരു സമഭുജ സാമാന്തരികത്തിന്റെ ശീർഷകങ്ങളായ ABCയിൽ AB, BC, AC എന്നീ വശങ്ങൾ ഒരു വൃത്തത്തെ യഥാക്രമം Z, X, Y എന്ന ബിന്ദുക്കളിൽ സ്പർശിക്കുന്നു.

<ZXY = 600 , <XZY = 500 ആയാൽ <A <B <C യുടെ അളവുകൾ കണ്ടെത്തുക.

25. A). രണ്ടു ഗോളങ്ങളുടെ അർദ്ധവ്യാസങ്ങളുടെ അനുപാതം 4: 3 ആണ്. (5)

(a) അവയുടെ ഉപരിതല വിസ്തീർണങ്ങളുടെ അനുപാതം കണ്ടെത്തുക. (1)

(b) ചെറിയ ഗോളത്തിന്റെ ഉപരിതല വിസ്തീർണം 144 cm2 ആണെങ്കിൽ, മറ്റേ ഗോളത്തിന്റെ ഉപരിതല വിസ്തീർണം കണ്ടെത്തുക. (2)

c) 4 സെ.മീ അർദ്ധവ്യാസമുള്ള ഒരു ഘനഗോളം ഉരുക്കി ഒരേ അർദ്ധവ്യാസമുള്ള രണ്ട് കോണുകളാക്കി മാറ്റുന്നു. ഓരോ കോണിന്റെയും ഉയരം കണ്ടെത്തുക. (2 )

        അല്ലെങ്കിൽ

B). ഒരു സമചതുര സ്തൂപിക താഴെ കാണുന്ന രീതിയിൽ ഒരു കാർഡ്‌ബോർഡ് ഉപയോഗിച്ച് നിർമ്മിച്ചിരിക്കുന്നു. ചതുരത്തിന്റെ ഓരോ വശവും 10 സെ.മീ ആണ്. ത്രികോണങ്ങളുടെ തുല്യവശങ്ങളുടെ നീളം 13 സെ.മീ ആണ്.

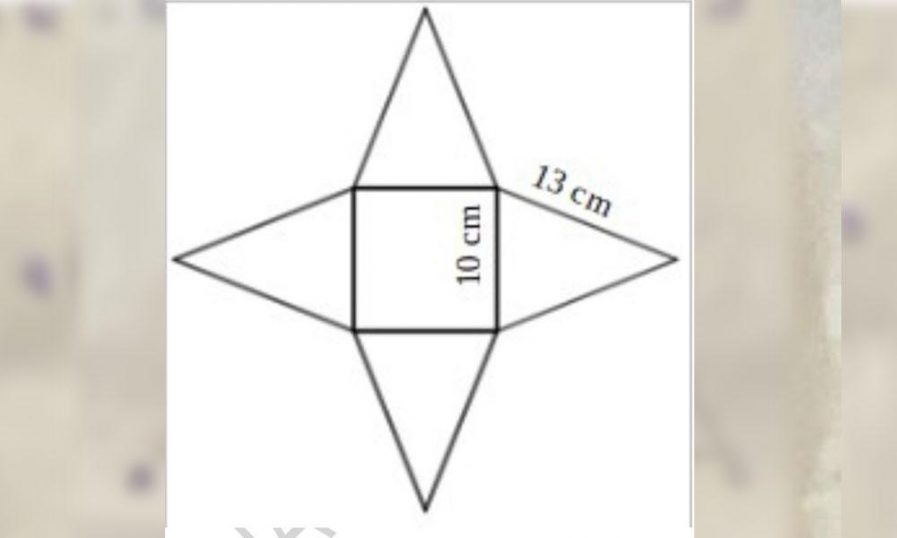
a) സമചതുര സ്തൂപിക ഉയരം കണ്ടെത്തുക. (1)

b) സമചതുര സ്തൂപികയുടെ ഉപരിതല പരപ്പളവ് കണക്കാക്കുക. (2)

c) സമചതുര സ്തൂപികയുടെ വ്യാപ്തം കണക്കാക്കുക. (2)

26. 3 സെ.മീ ആരമുള്ള ഒരു ത്രികോണം നിർമ്മിക്കുക. അതിലെ രണ്ട് കോണുകൾ 32½0 ഉം 37½0 ഉം ആണ്. (3)

27. വീതി 5 സെ. മീറ്ററും ഉയരം 4 സെ. മീറ്ററമുള്ള ഒരു ദീർഘചതുരം വരയ്ക്കുക. അതേ വിസ്തീർണമുള്ള, വീതി 6 സെ. മീ ആയ ഒരു ചതുരം നിർമിക്കുക. (4)

28. 4 സെ.മീ ആരമുമുള്ള ഒരു വൃത്തം വരയ്ക്കുക. വൃത്തകേന്ദ്രത്തിൽ നിന്ന് 7.5 സെ.മീ അകലെയുള്ള ഒരു ബിന്ദു അടയാളപ്പെടുത്തുക. ആ ബിന്ദുവിൽ നിന്ന് വൃത്തത്തിലേക്കുള്ള തൊടുവരകൾ (Tangents) വരയ്ക്കുക. (4)